Solved Examples on Logarithmic Models
Calculators: Logarithmic Models Calculator
Answer all questions using at least one approach.
Because the
second approach: technology using the TI84/84-Plus is widely used,
we shall use it to solve most of the questions, unless stated otherwise.
(1.) Determine a logarithmic function to model the data.
Select the correct answer choice.
Review the Second Approach: Step-by-step screenshots of how to use the TI-84 Plus to determine Logarithmic Regression Equation
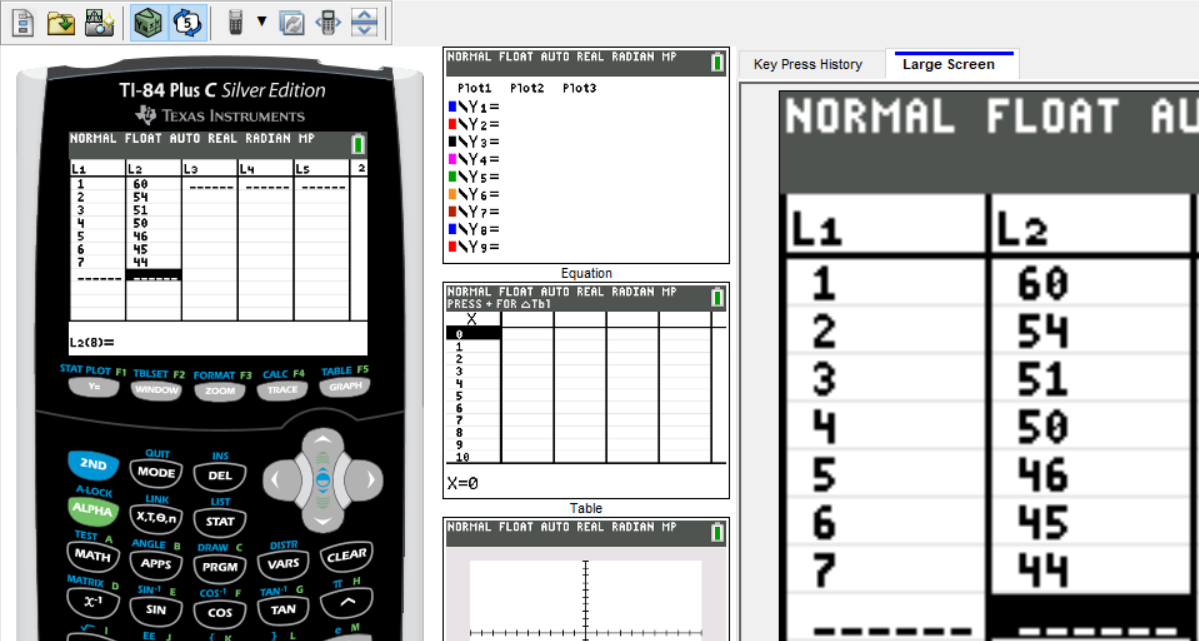
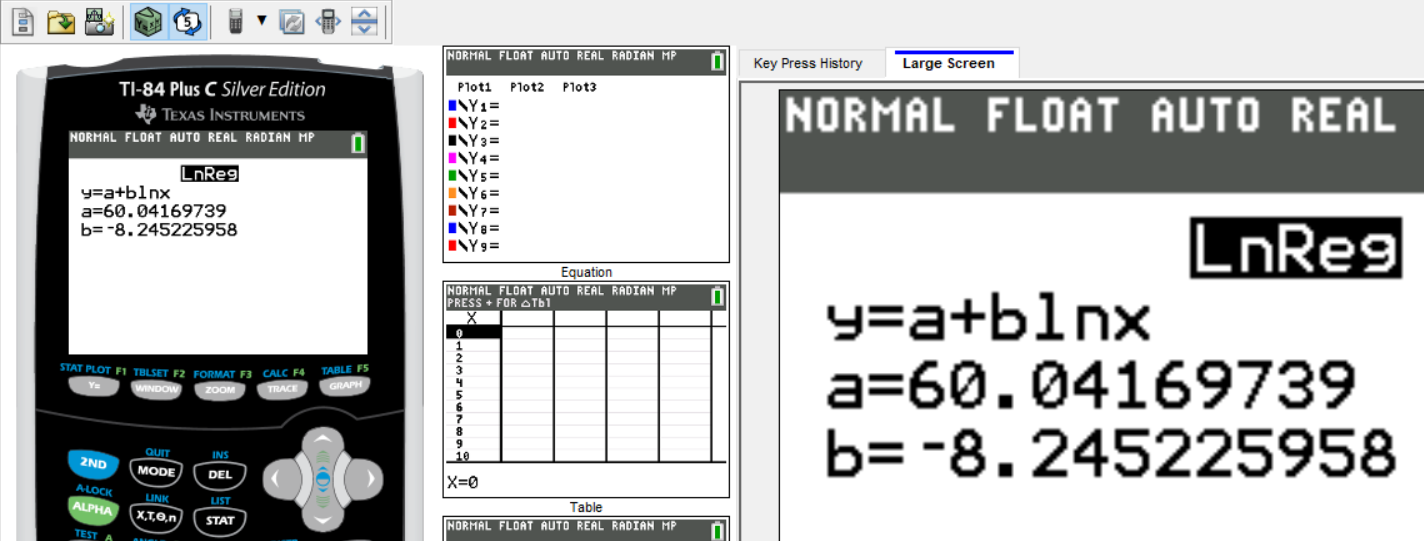
$ y = a + b\ln x \\[3ex] y = 60.04169739 + -8.245225958 \ln x \\[3ex] y = 60.04169739 - 8.245225958 \ln x \\[3ex] y \approx 60.04 - 8.25 \ln x ...nearest\;\;hundredth $
| x | y |
|---|---|
| $1$ | $60$ |
| $2$ | $54$ |
| $3$ | $51$ |
| $4$ | $50$ |
| $5$ | $46$ |
| $6$ | $45$ |
| $7$ | $44$ |
Select the correct answer choice.
- $f(x) = 60.73(0.95)x$
- $f(x) = 0.93(60.73)x$
- $f(x) = 60.04 - 8.25\ln x$
- $f(x) = 8.25 - 60.04\ln x$
Review the Second Approach: Step-by-step screenshots of how to use the TI-84 Plus to determine Logarithmic Regression Equation


$ y = a + b\ln x \\[3ex] y = 60.04169739 + -8.245225958 \ln x \\[3ex] y = 60.04169739 - 8.245225958 \ln x \\[3ex] y \approx 60.04 - 8.25 \ln x ...nearest\;\;hundredth $
(2.) Determine the logarithmic regression of the data below using either a calculator or spreadsheet program.
Then, estimate the x-value when the y-value is 5.2
Round your answer to one decimal place.
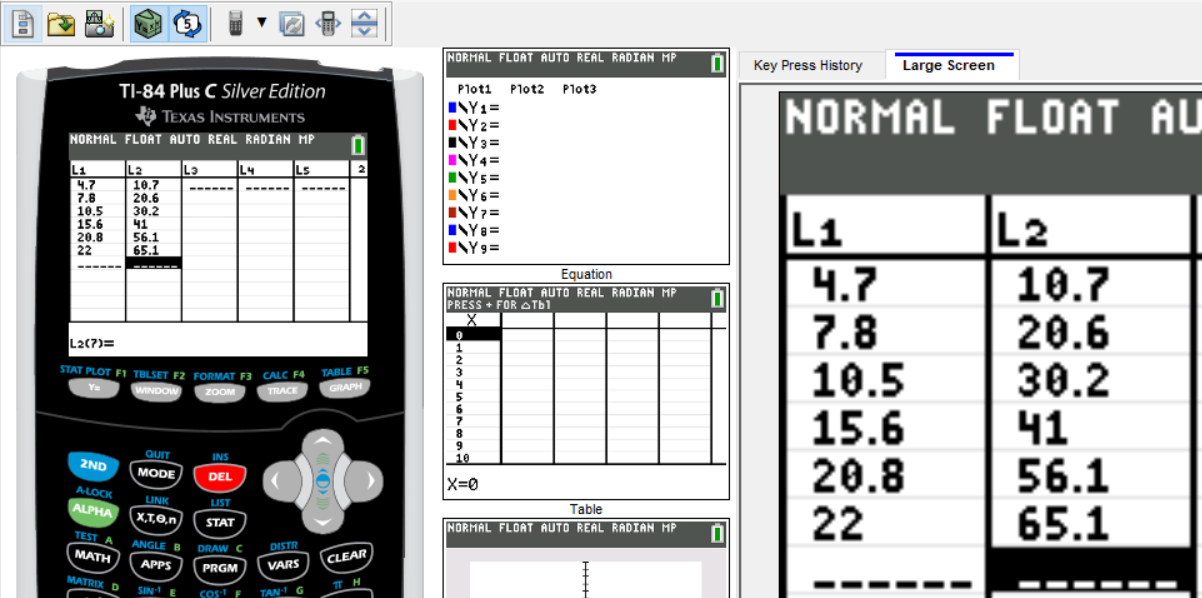
Review the Second Approach: Step-by-step screenshots of how to use the TI-84 Plus to determine Logarithmic Regression Equation
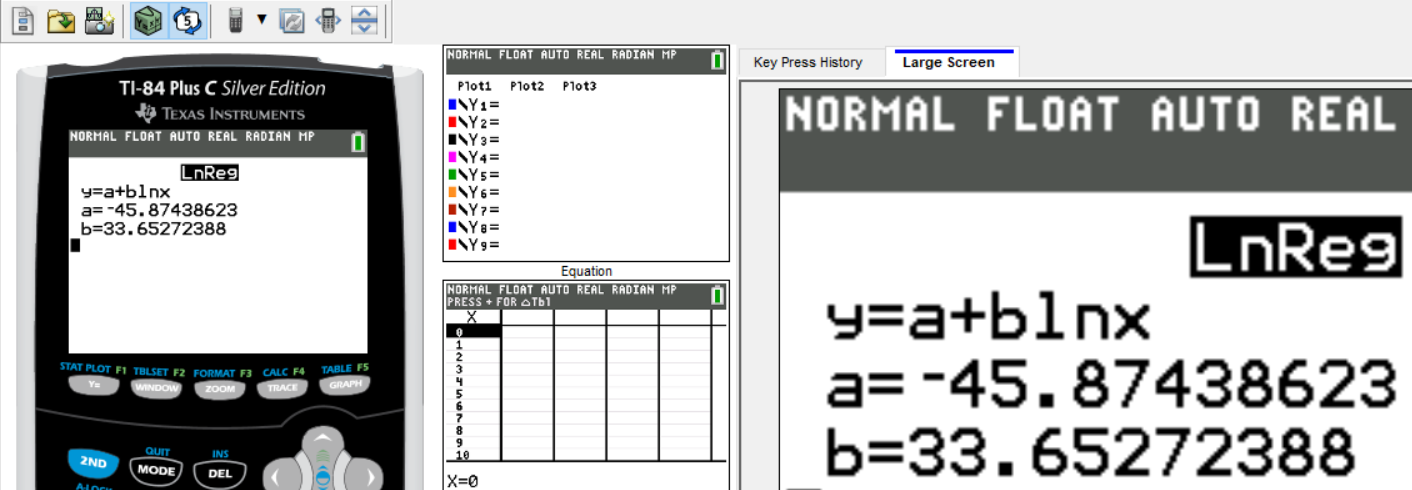
$ y = a + b\ln x \\[3ex] y = -45.87438623 + 33.65272388 \ln x \\[3ex] y \approx -45.9 + 33.7 \ln x ...one\;\;decimal\;\;place \\[3ex] when\;\;y = 5.2 \\[3ex] 5.2 = -45.87438623 + 33.65272388 \ln x \\[3ex] -45.87438623 + 33.65272388 \ln x = 5.2 \\[3ex] 33.65272388 \ln x = 5.2 + 45.87438623 \\[3ex] 33.65272388 \ln x = 51.07438623 \\[3ex] \ln x = \dfrac{51.07438623}{33.65272388} \\[5ex] \ln x = 1.517689516 \\[3ex] e^{\ln x} = e^{1.517689516} \\[3ex] x = 4.561673338 $
Then, estimate the x-value when the y-value is 5.2
Round your answer to one decimal place.
| x | y |
|---|---|
| $4.7$ | $10.7$ |
| $7.8$ | $20.6$ |
| $10.5$ | $30.2$ |
| $15.6$ | $41$ |
| $20.8$ | $56.1$ |
| $22$ | $65.1$ |
Review the Second Approach: Step-by-step screenshots of how to use the TI-84 Plus to determine Logarithmic Regression Equation


$ y = a + b\ln x \\[3ex] y = -45.87438623 + 33.65272388 \ln x \\[3ex] y \approx -45.9 + 33.7 \ln x ...one\;\;decimal\;\;place \\[3ex] when\;\;y = 5.2 \\[3ex] 5.2 = -45.87438623 + 33.65272388 \ln x \\[3ex] -45.87438623 + 33.65272388 \ln x = 5.2 \\[3ex] 33.65272388 \ln x = 5.2 + 45.87438623 \\[3ex] 33.65272388 \ln x = 51.07438623 \\[3ex] \ln x = \dfrac{51.07438623}{33.65272388} \\[5ex] \ln x = 1.517689516 \\[3ex] e^{\ln x} = e^{1.517689516} \\[3ex] x = 4.561673338 $