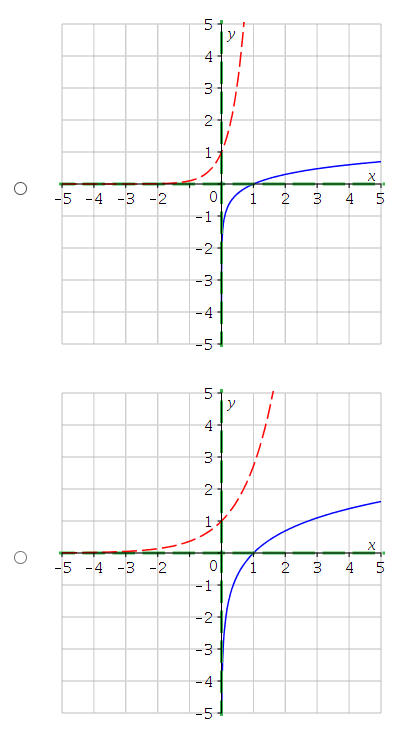
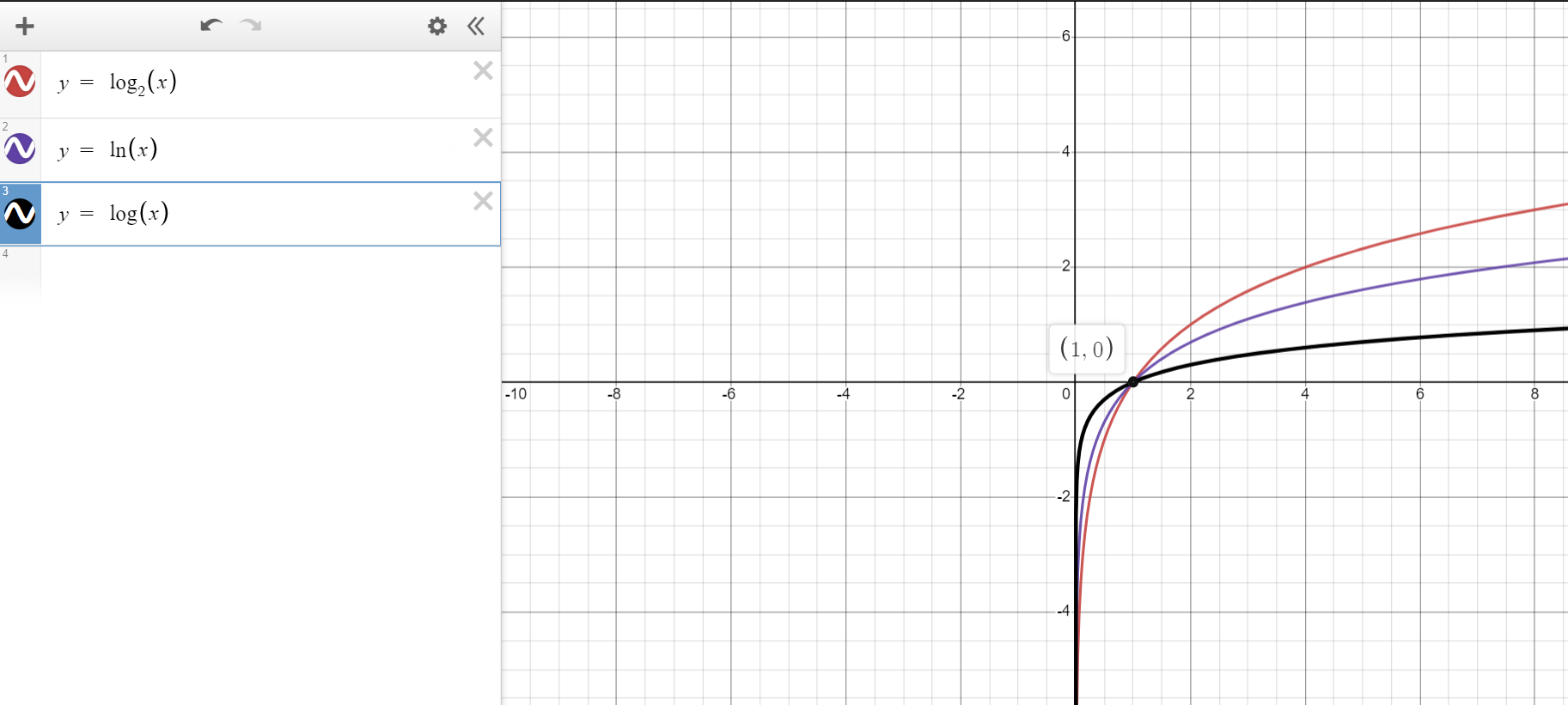
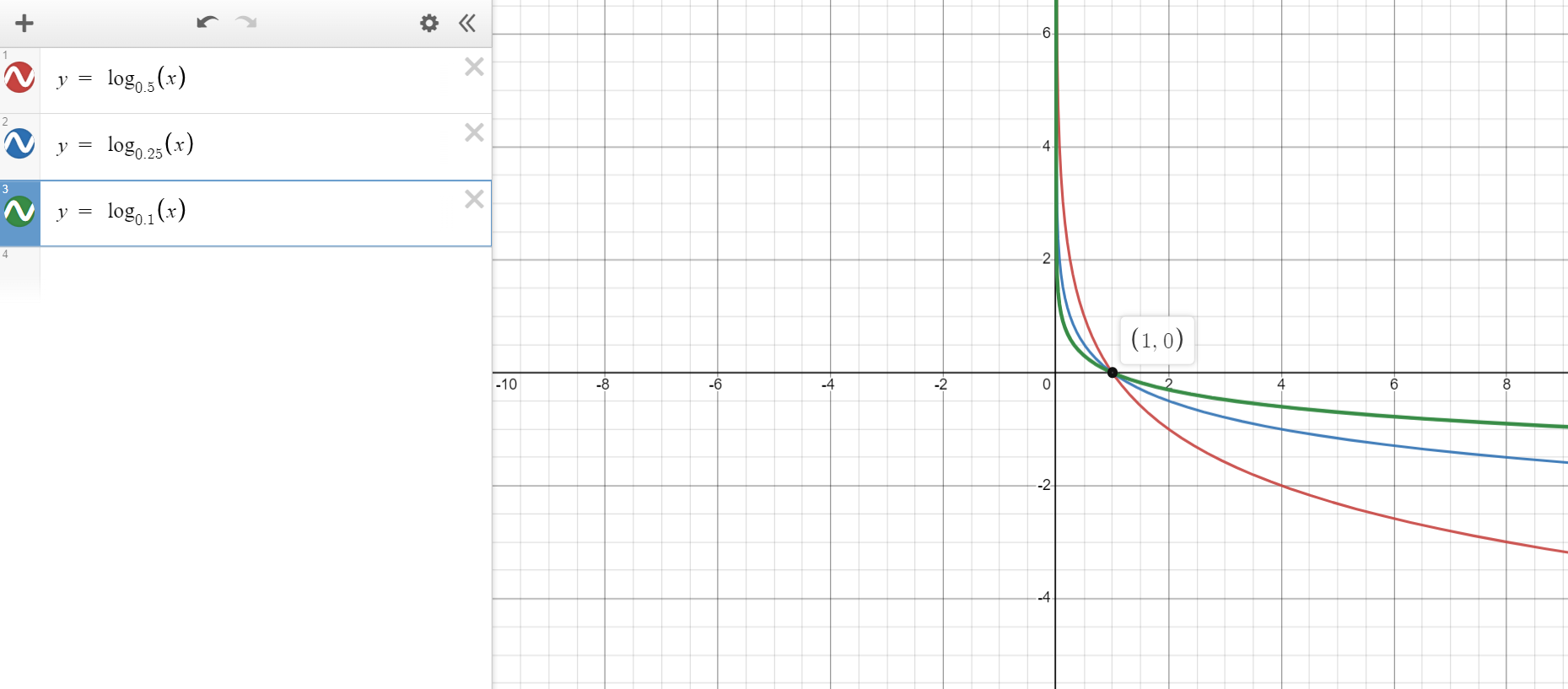
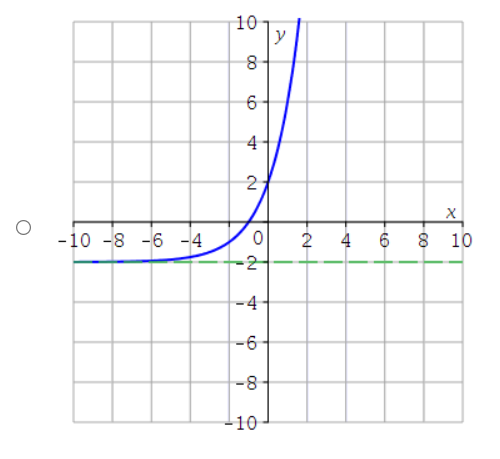
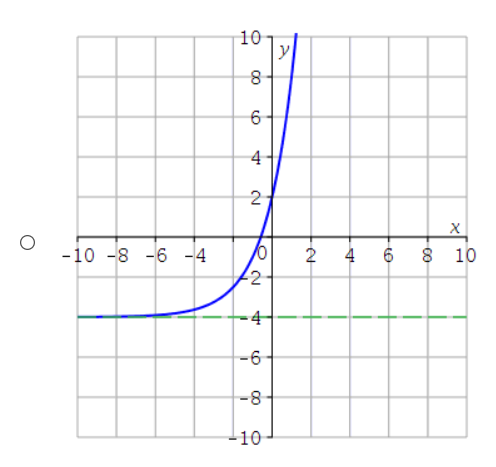
(3.) All the graphs shown below have the form: $f(x) = ab^x$
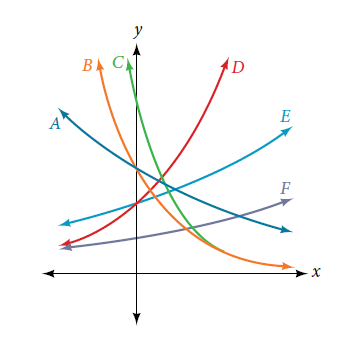
(a.) Which graph has the smallest value of $a$?
(b.) Which graph has the largest value of $a$?
(c.) Which graph has the smallest value of $b$?
(d.) Which graph has the largest value of $b$?
(a.)
The graph with the smallest value of $a$ is the graph with the least $y-intercept$
This implies that when $x = 0$, the graph that has the least value of $y$ (the least value of $y$ on the $y-axis$) is the graph with the smallest value of $a$
That graph is Graph F
(b.)
The graph with the largest value of $a$ is the graph with the greatest $y-intercept$
This implies that when $x = 0$, the graph that has the greatest value of $y$ (the greatest value of $y$ on the $y-axis$) is the graph with the largest value of $a$
That graph is Graph C
(c.)
The graph with the samllest value of $b$ is the graph that:
(1.) decreases from left to right.
It is a decreasing function which signifies an exponential decay.
and
(2.) has the steepest slope.
The first condition eliminates Graphs D, E, F because those graphs are increasing from left to right and their bases are greater than 1
We are left with Graphs A, B, C
These graphs are decreasing from left to right. Their bases are between 0 and 1
Looking at these graphs, the one with the steepest slope is Graph C
Therefore, Graph C has the smallest value for the base, $b$
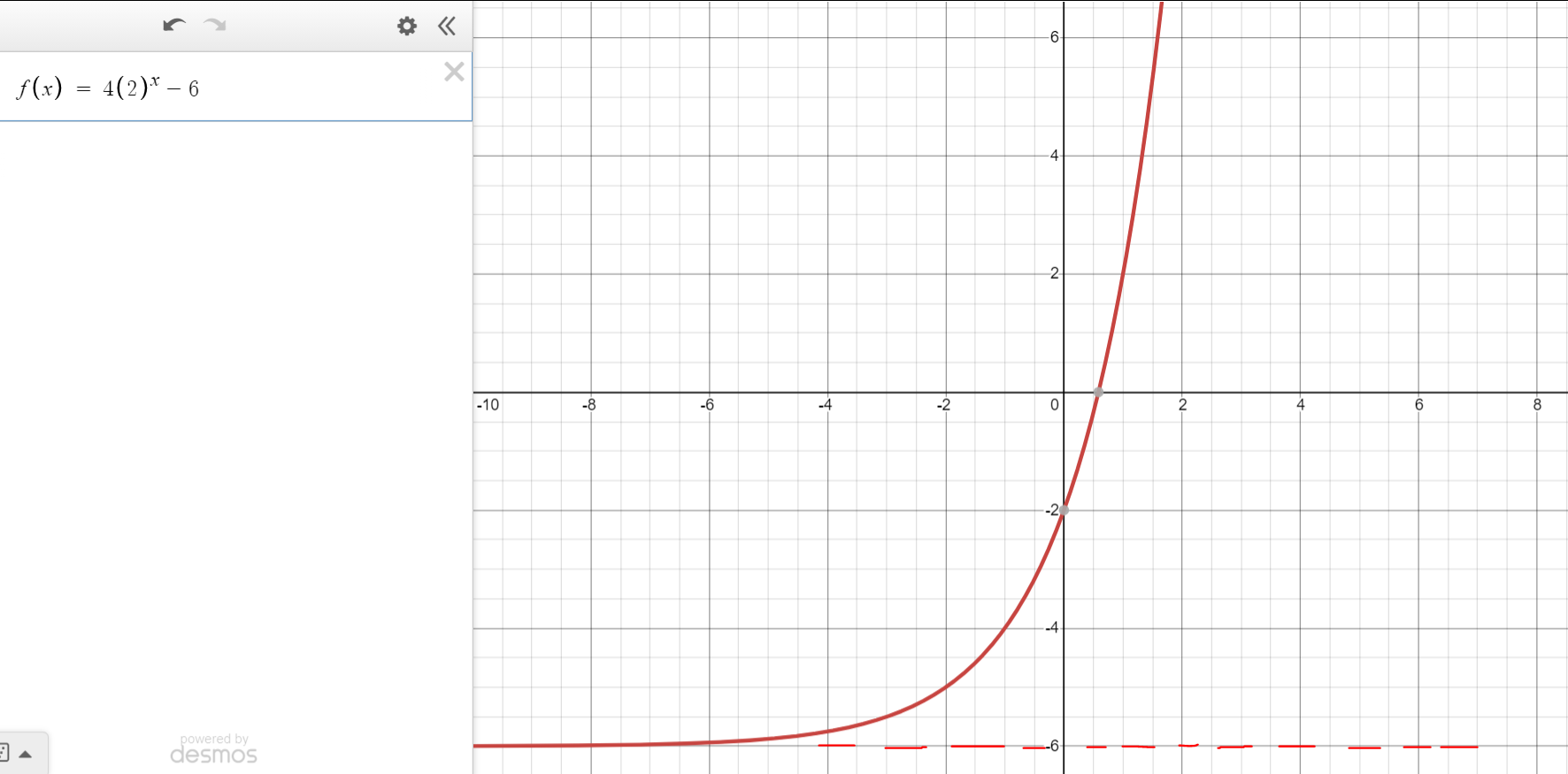
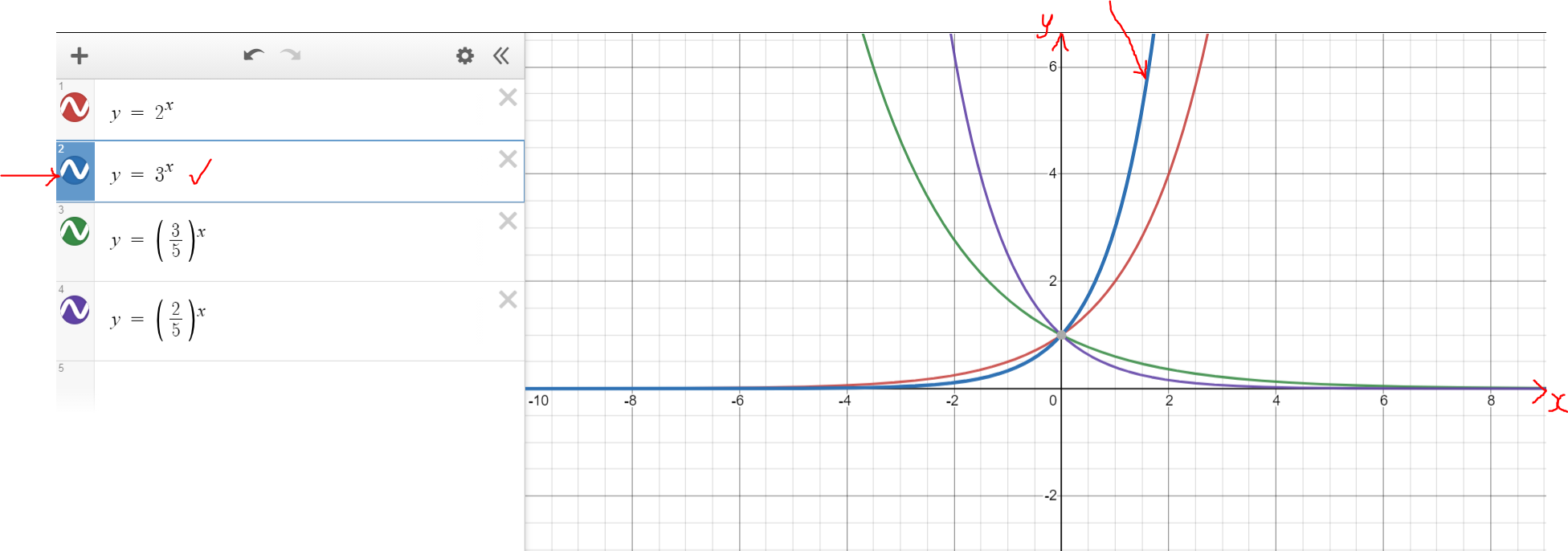
Let us verify with some graph examples:

(d.)
The graph with the largest value of $b$ is the graph that:
(1.) increases from left to right.
It is an increasing function which signifies an exponential growth.
and
(2.) has the steepest slope.
The first condition eliminates Graphs A, B, C because those graphs are decreasing from left to right and their bases are between 0 than 1
We are left with Graphs D, E, F
These graphs are increasing from left to right. Their bases are greater than 1
Looking at these graphs, the one with the steepest slope is Graph D
Therefore, Graph D has the largest value for the base, $b$
Let us verify with some graph examples:

(a.) Which graph has the smallest value of $a$?
(b.) Which graph has the largest value of $a$?
(c.) Which graph has the smallest value of $b$?
(d.) Which graph has the largest value of $b$?
(a.)
The graph with the smallest value of $a$ is the graph with the least $y-intercept$
This implies that when $x = 0$, the graph that has the least value of $y$ (the least value of $y$ on the $y-axis$) is the graph with the smallest value of $a$
That graph is Graph F
(b.)
The graph with the largest value of $a$ is the graph with the greatest $y-intercept$
This implies that when $x = 0$, the graph that has the greatest value of $y$ (the greatest value of $y$ on the $y-axis$) is the graph with the largest value of $a$
That graph is Graph C
(c.)
The graph with the samllest value of $b$ is the graph that:
(1.) decreases from left to right.
It is a decreasing function which signifies an exponential decay.
and
(2.) has the steepest slope.
The first condition eliminates Graphs D, E, F because those graphs are increasing from left to right and their bases are greater than 1
We are left with Graphs A, B, C
These graphs are decreasing from left to right. Their bases are between 0 and 1
Looking at these graphs, the one with the steepest slope is Graph C
Therefore, Graph C has the smallest value for the base, $b$
Let us verify with some graph examples:

(d.)
The graph with the largest value of $b$ is the graph that:
(1.) increases from left to right.
It is an increasing function which signifies an exponential growth.
and
(2.) has the steepest slope.
The first condition eliminates Graphs A, B, C because those graphs are decreasing from left to right and their bases are between 0 than 1
We are left with Graphs D, E, F
These graphs are increasing from left to right. Their bases are greater than 1
Looking at these graphs, the one with the steepest slope is Graph D
Therefore, Graph D has the largest value for the base, $b$
Let us verify with some graph examples:

(4.) GCSE Leo wants to draw the graph of $y = 2^x$ for values of x from 0 to 4
Here is his graph.
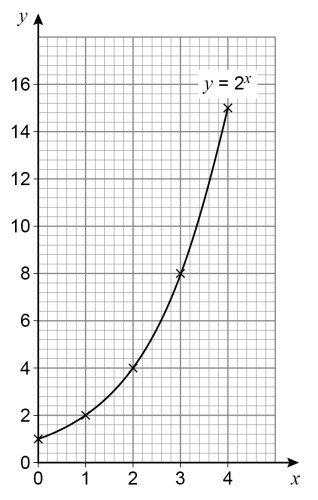 Make one criticism of his graph.
Make one criticism of his graph.
$ When\;\;x = 4,\;\;y = 2^4 = 16 \\[3ex] $ However, Leo did not label the y-value correctly for an x-value of 4
Here is his graph.

$ When\;\;x = 4,\;\;y = 2^4 = 16 \\[3ex] $ However, Leo did not label the y-value correctly for an x-value of 4